Two weekends ago, DevCon held its Code Challenge Cup (C-Cup) at Xavier School Greenhills.
Now while I am the current VP for Technology of the said group and spent 6 hours painstakingly checking a good chunk of the submissions, I wasn’t involved in the making of the problems (I was the tech support guy, not a “judge”). I didn’t even look at the problems until it was linked to on the event page days after the event.
Anyway, being a sucker for computer science problems I’ve decided to solve all of them on my own. And given that nobody used Ruby at the event, I going to use Ruby to solve them.
Note that while I’ve confirmed that the solutions below pass the judges’ test cases, they are not (yet) endorsed by any of the judges in the event.
Oh, and yeah, to back up my claim that Quiwa’s Data Structures will allow you to solve most of the problems in programming competitions, I’ve included references to the said book in the solutions below.

Problem A: Best-Fit Lines
Problem Type: Statistics
My solution:
While this problem can be solved with some difficulty using brute-force, going through all possibilities of a and b in 0.001 steps, the formula for this problem (simple linear regression) is pretty straightforward.
A few things to note about the code above:
- I use
String#strip()in all of the problems just to be sure. I don’t really need to do it. - Truncate is preferred over rounding (even though both will get full points) but Ruby doesn’t have a built-in truncate function. And so I had to make one.
- Unlike Python, Ruby doesn’t have a built-in
sum()function. Using a fullreduce()works fine but I don’t like the syntax so I chose a map–reduce form instead.
Problem B: Weird Writing
Problem Type: Coding
My solution:
This is what I’d call a “coding problem”. There are no Computer Science or Math related tricks here; the problem can be solved by anyone who knows the basics of programming e.g. basic data structures, string manipulation, and sorting.
The lines 20 – 26 above can be confusing for non-Ruby or non-Perl programmers due to the amount of small things done per line. Let’s translate it one by one:
Line 20 creates a translation table/hash which we’ll use to translate the words.
alphabet.split(//)– converts the string to a character array, as Ruby does not have this built in.zip('A'..'Z')– “zips” the array with the real alphabet creating an array like[["Q", "A"], ["W", "B"]...]Hash[*...flatten]– flattens the array so we could turn it into a Hash e.g.{ "Q" => "A", "W" => "B", ...}
Line 21 – 24 creates a new array containing word pairs consisting of the input words and their equivalent words in the Ripley alphabet.
word_pairs = words.map do |word|– maps the entire array to a new array based on the return value of the blockword.split(//)– again, converts the string to a character array.map { |c| translation_table[c] }.join– maps each character to the Ripley alphabet using the hash we made earlier. Thejointurns the array back to a string[word, ...]– return value of the block is the word pair array e.g.["SCOTT", "RVIEE"]
After line 24 you now have an array like [["SCOTT", "RVIEE"], ["WEAVER", "BCSWCD"]]. We then sort this list by the second element of the pair (i.e. .sort_by { |pair| pair[1] }) and put each word on the output file (i.e. .each { |pair| output.puts pair[0] })
Problem C: Congressional Progression
Problem Type: Graph Theory
My solution:
This is the first problem whose solution you could find in Data Structures. A major district in the problem is a vertex, once removed, produces a graph where there is no path between one or more pairs of vertices. This can easily be determined once you have a transitive closure for the graph, which we will construct using Warshall’s algorithm.
The code above a bit straightforward:
- Line 24 simply removes all of the edges that contain the currently tested major district / vertex
- Lines 25 – 28 looks fancy, but all it does is create a translation table for the name of the district with their respective positions e.g.
{ "Borgia" => 0, "Camelville" => 1 } - Lines 33 – 45 is a direct translation of the Warshall’s Algorithm from the book to Ruby
- Line 46 determines if the district is major by checking for the existence of
falses in the adjacency matrix.
Data Structures reference: page 331, Warshall’s Algorithm
Problem D: Islands
Problem Type: Graph Theory
My solution:
This problem can be solved in many ways, with the simplest being graph traversal algorithms. And the simplest of those is depth-first search which is used by the code above.
To summarize what the code above does:
- Look for an island tip closest to the top.
- Increment the island count.
- Use DFS to delete the island piece by piece.
- Repeat until there are no islands left.
Data Structures reference: page 253, Depth-First Search
Problem E: Basketball
Problem Type: Coding
My solution:
Another coding problem. Expect to fail many technical interviews if you can’t program this in less than 30 minutes.
The existence of Array#count() makes this problem too easy in Ruby.
Problem F: Utility Maximization
Problem Type: Mathematical Optimization / Microeconomics
My solution:
Like Problem A, this problem can be solved either through brute-force or having knowledge of microeconomics or mathematical optimization.
And it can be solved using blind luck.
To explain why it can be solved through luck, we must first look at a “real” solution using Lagrange multipliers:
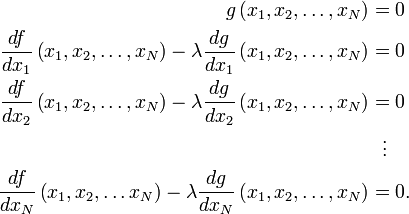
Not fun, right?
However, if you set the function and constraint to the ones given in the problem and take time to solve the partial differential equations, you’ll end up with something like:
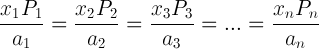
If you were lucky, you could’ve seen this pattern in the examples:
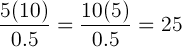
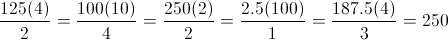
In short, the price x quantity of each good is proportional to their substitutability scale. From there, it should not be hard to derive:
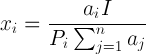
i.e. line 18 above.
Problem G: Evolution of Industries
Problem Type: Graph Theory
My solution:
We need to find the path between two points in the graph that produces the highest probability. Calculating probability of independent events is simple (just multiply them all together) while finding the path is only a matter of choosing which pathfinding algorithm to choose. For the code above, I chose the most common algorithm: Dijkstra’s Algorithm.
Line 24 onwards is a direct implementation of the algorithm from the book.
Data Structures reference: page 312, Dijkstra’s Algorithm
Problem H: Relatively Prime
Problem Type: Number Theory
My solution:
The easiest problem of the set. All it takes is for you to know how to calculate the GCF of two numbers efficiently. If you’re not using Ruby or Python (which has built in GCD functions), you can code the Euclidian Algorithm in less than a minute.
Data Structures reference: page 5, Euclid’s Algorithm
Problem I: Jugs
Problem Type: Graph Theory
My solution:
This classic puzzle isn’t that hard when you use graph-traversal algorithms on it. Since we’ve already used DFS and Dijkstra’s algorithm above, I chose to use Breadth-First Search this time around. (Note that DFS is fine because there’s no “shortest path” requirement.)
Here’s how BFS can be used to solve the first example, 3 5 4:
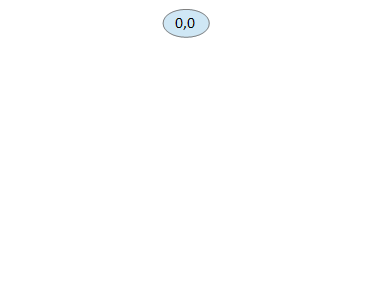
We start with our first node, representing 0 gallons for jug A and 0 gallons for jug B.
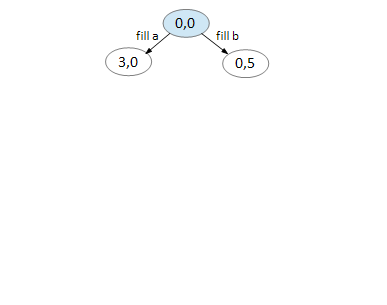
We can only do two things, fill A and fill B. All other moves returns you to the same node.
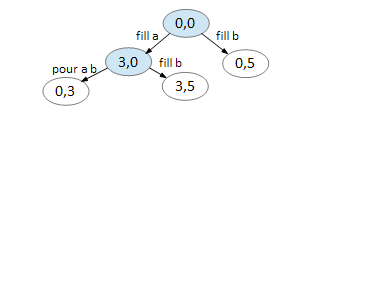
On node (3,0), we can fill B and pour A B. Again, all else returns you to a previously visited node.
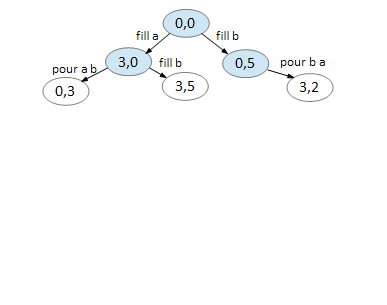
On node (0,5), we can only fill A and pour B A. Note that (3,5) has already been created in the previous step.
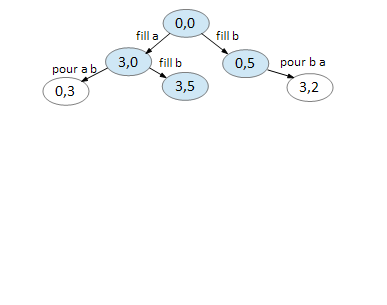
Node (3,5) is a dead end.
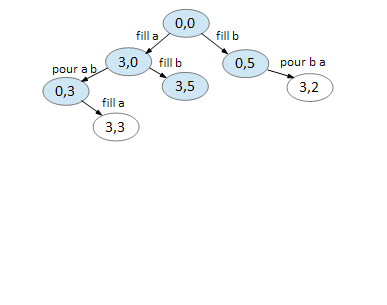
On node (0,3), we can fill A.
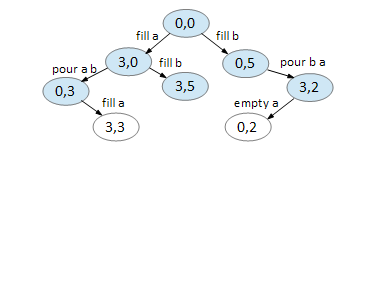
On node (3,2), we can empty A.
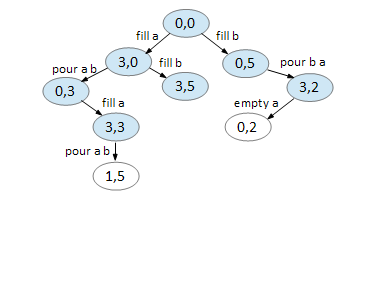
On node (3,3), we can pour A B.
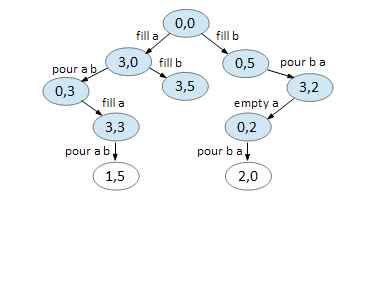
On node (0,2), we can pour B A.
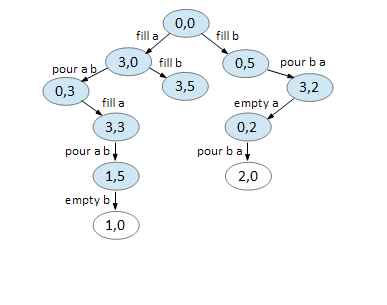
On node (1,5), we can empty B.
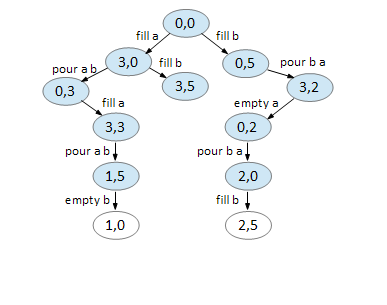
On node (2,0), we can fill B.
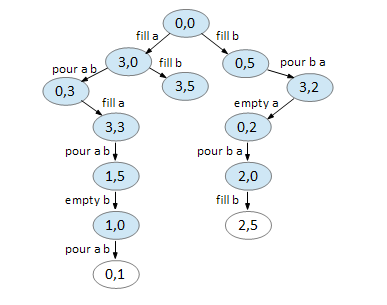
On node (1,0), we can pour A B.
On node (2,5), we can pour B A leaving 4 gallons on jug B.
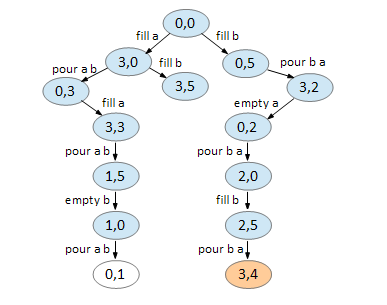
Backtracking, we now have our solution.
The whole thing, animated:
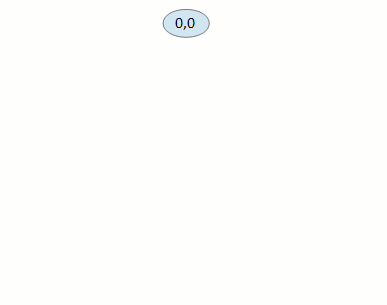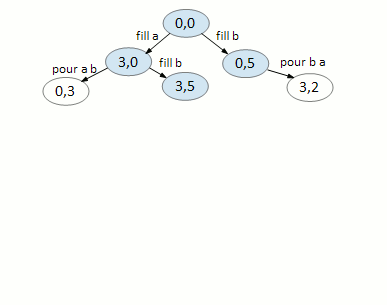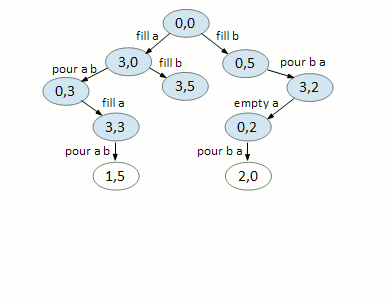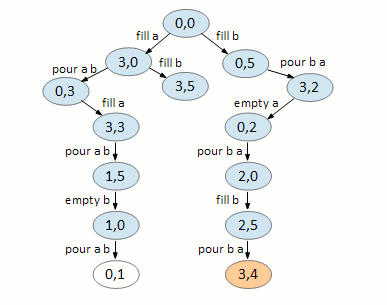
My BFS implementation is kinda weird in that it doesn’t use a real queue (it uses a simple array) and we store the back edges along with the action in a hash of a hash.
The solution above also finds the solution for putting N gallons in jug B. According to the spec, you only need to put the water in either jug. We’ll just leave modifying the solution above to do this as your assignment.
Data Structures reference: page 265, Breadth-First Search
Problem J: Just the Facts
Problem Type: Coding
My solution:
Last and probably one of the least, we have this coding problem.
Your main problem here is how to calculate factorials – using normal integers, you’ll get to the integer limit very quickly. There are many clever ways of calculating the last non-zero digit of a factorial, but there’s really no need to do that. Using arbitrary-precision arithmetic (e.g. Java’s BigInteger) you can calculate 10000! in all of the given languages in less than a second using less than 1MB of memory.
Here’s what we did in the Ruby code above:
(1..n).reduce(:*)– calculate factorial usingreduce(). Ruby automatically converts integers toBignumwhen they reach a certain size..to_s.gsub("0", "")– convert factorial to string and replace all 0’s with blanks[-1]– get the last character
—
And that’s that. To summarize, we got
- 3 problems that can be solved with minimal CS instruction
- 5 that can be solved using Quiwa’s Data Structures
- 2 niche statistics and economics problems (A and F)
In other words, it’s a pretty good problem set for programmers of all levels. I might even go as to say that, given enough time, a second-year Computer Science student should be able to answer 8 of them armed only with a laptop, their textbooks, and a complete programming language API.


